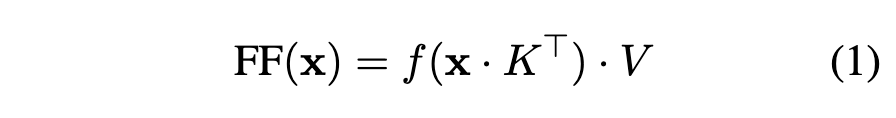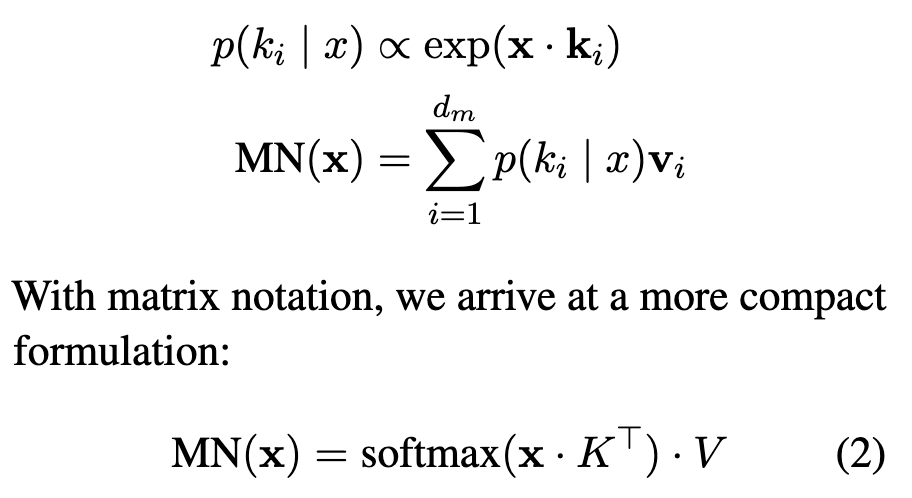This is the master note for Mechanistic Interpretability
what
- reverse engineering the computational mechanism and representation learnt by neural networks to human-understandable algorithms and concepts1
- a paradigm shift in interpretability: surface-level analysis (input/output relations) → inner interpretability (internal mechanisms) 1
- similar to the shift from behaviourism to cognitive neuroscience in psychology
- Mech Interp is an approach toward inner interpretability
Link to original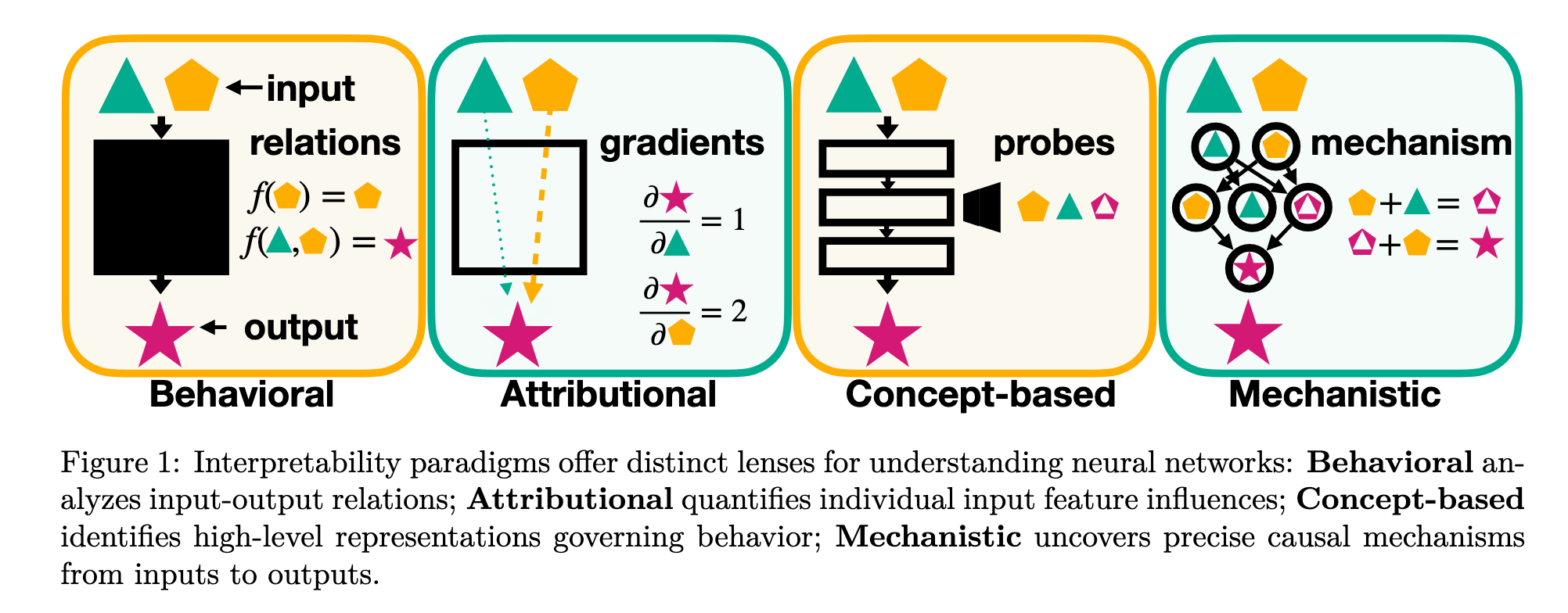
some terminologies
- Features:
- Neurons 1
- are computational units
- potentially representing individual features
- forming privileged bases
- Circuit
- sub-graphs of the network, consisting of features and the weights connecting them
- monosemantic and polysemantic neurons
- monosemantic: neurons corresponding to a single semantic concept
- polysemantic: neurons associated with multiple, unrelated concepts
- if neurons were the fundamental primitives of model representations
- all neurons would be monosemantic
- implying a 1-to-1 relation between neurons and features
- however, empirical studies observed that neurons are polysemantic
- Privileged bases
- the standard bases of the representation space
Link to original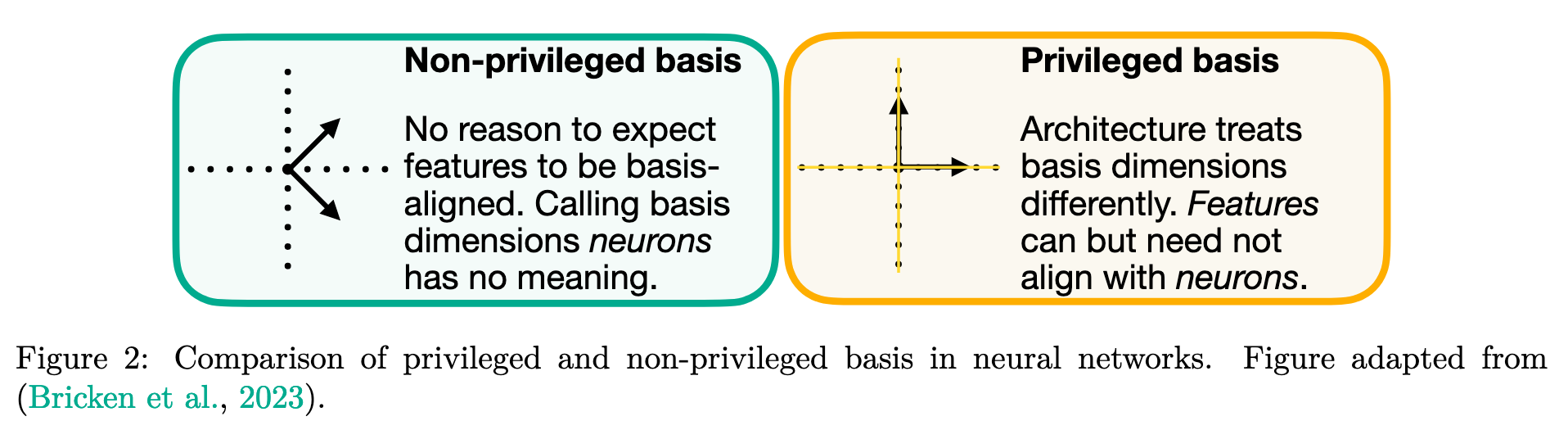
- the standard bases of the representation space
hypotheses
Linear representation hypothesis
- Features / concepts are represented by orthogonal directions in activation space
- but need not be aligned with the privileged bases
- The network represents features as linear combinations of neurons
Link to original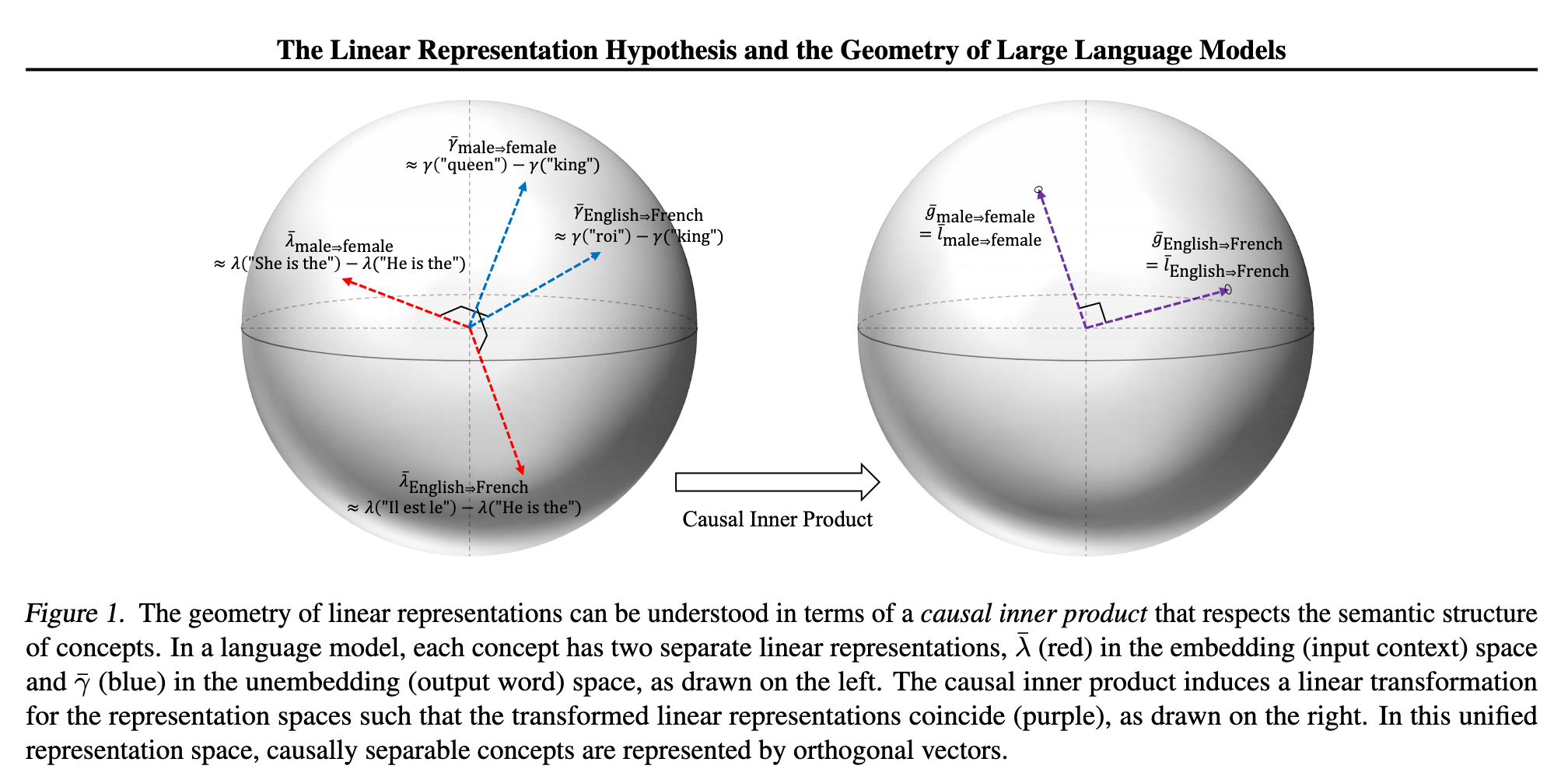
Superposition Hypothesis
- The representation may encode features not with the basis directions (neurons) but with possible almost orthogonal directions.
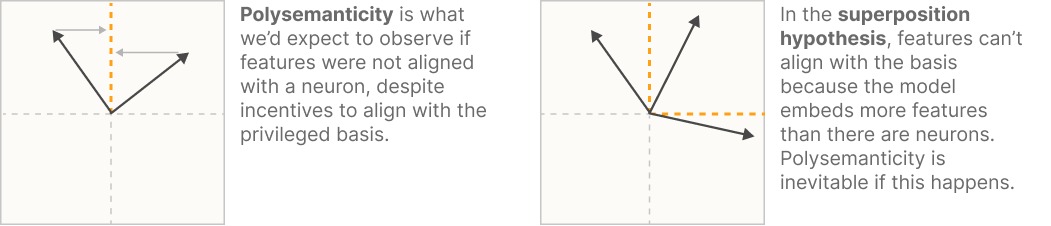
- Neural networks represent more features than they have neurons by encoding features in ovelapping combination of neurons 1
Link to original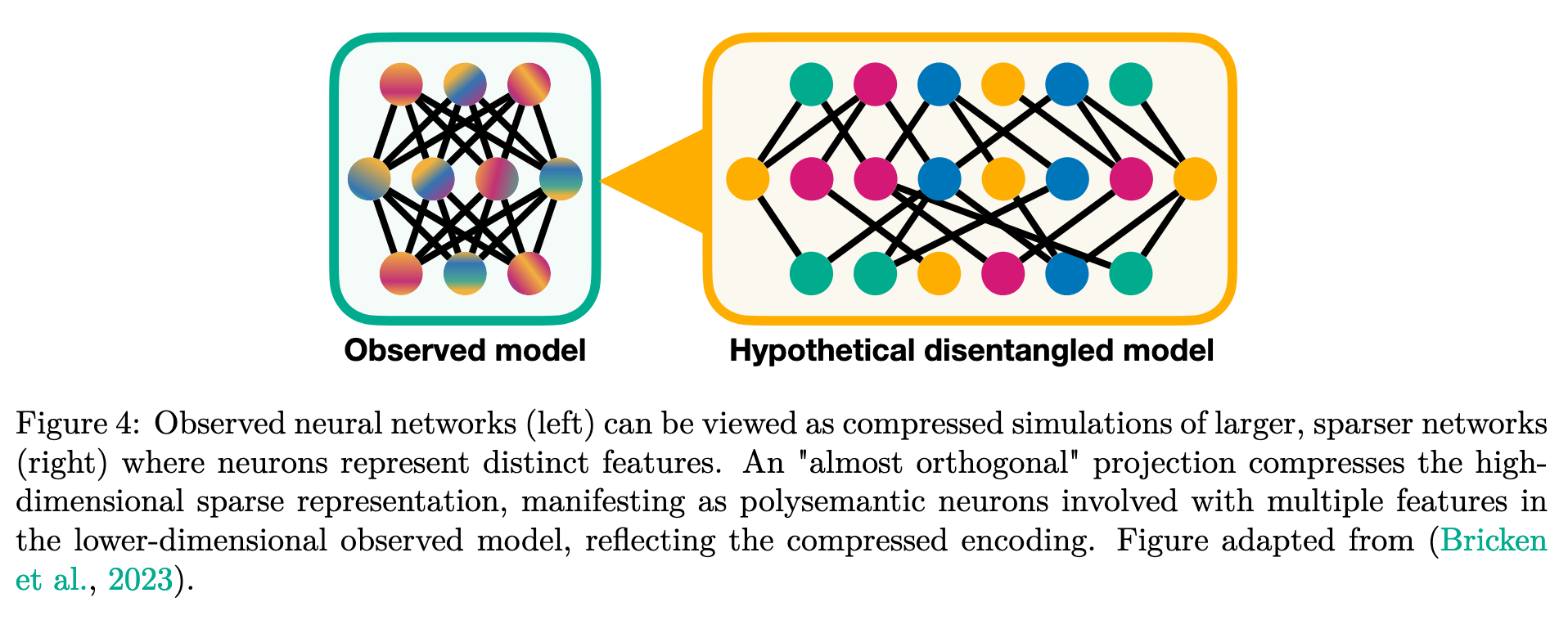
- Non-orthogonality means that features interfere with one another.
- Sparsity means that a feature rarely occurs. The assumption is most features are sparse.
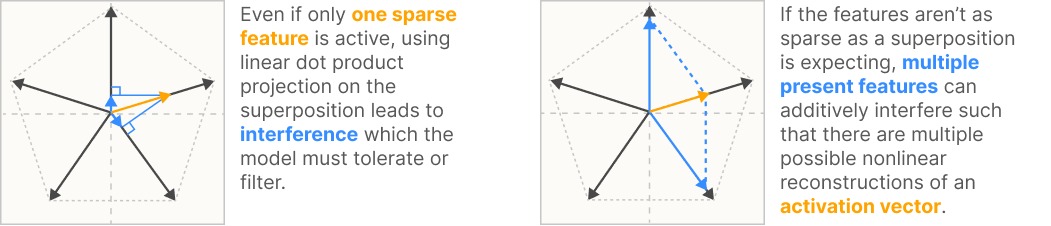
Toy model of superposition
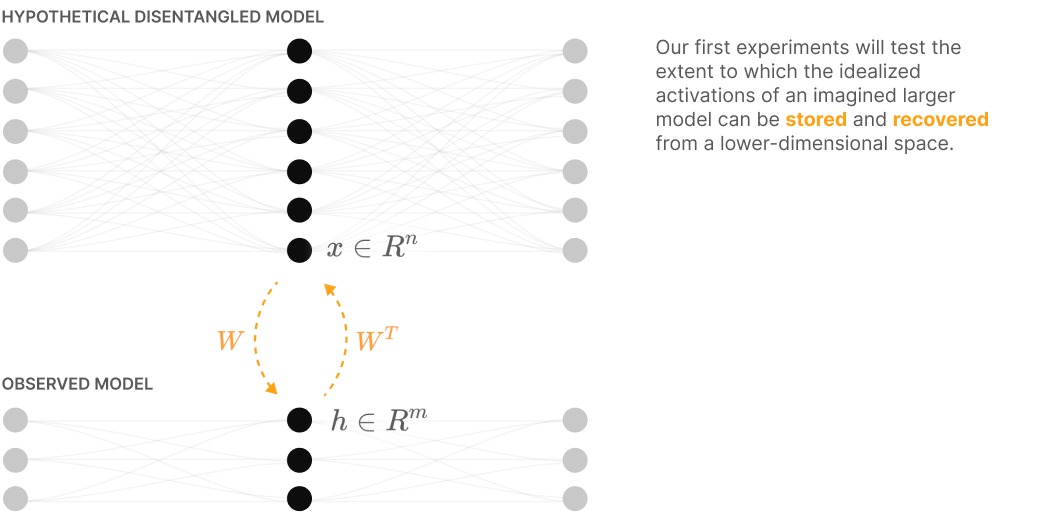
Link to original
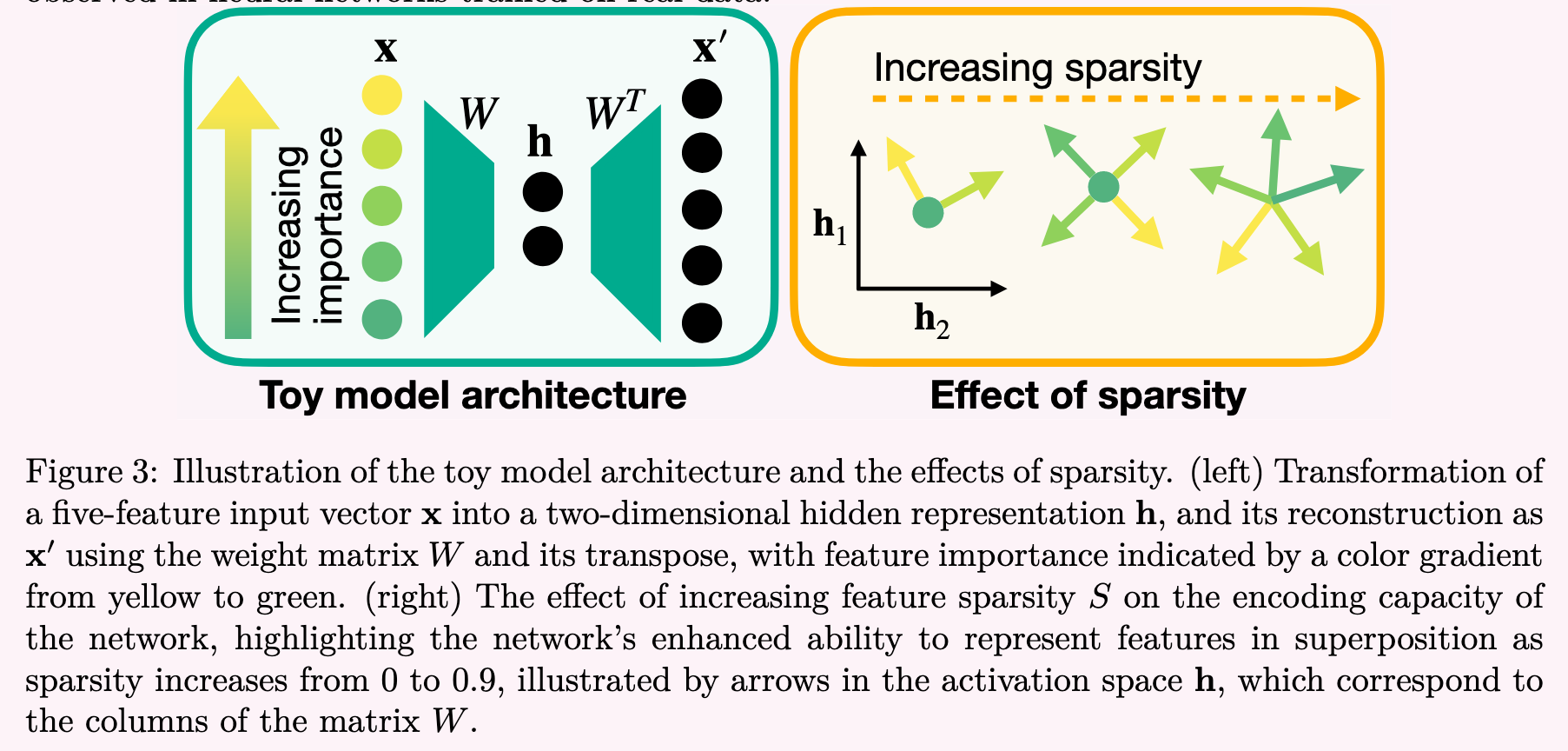
A Hierarchy of Feature Properties3
4 progressively more strict properties that neural network representations might have:
- Decomposability: Neural network activations which are decomposable can be decomposed into features, the meaning of which is not dependent on the value of other features.
- Linearity: Features correspond to directions. Each feature has a corresponding representation direction . The presence of multiple features activating with values is represented by
- Superposition vs Non-Superposition: A linear representation exhibits superposition if is not invertible. If is invertible, it does not exhibit superposition.
- Basis-Aligned: A representation is basis aligned if all are one-hot basis vectors. A representation is partially basis aligned if all are sparse. This requires a privileged basis.
The first two are hypothesized to be widespread, while the latter are believed to be occured only sometimes.
Universality hypothesis
- Analogous features and circuits form across model and tasks.
A mechanistic view on LLM
Virtual Weights and the Residual Stream as a Communication Channel 4
- View the residual stream as the main object that accumulate information

- MLP and Attention are branches that write to the stream
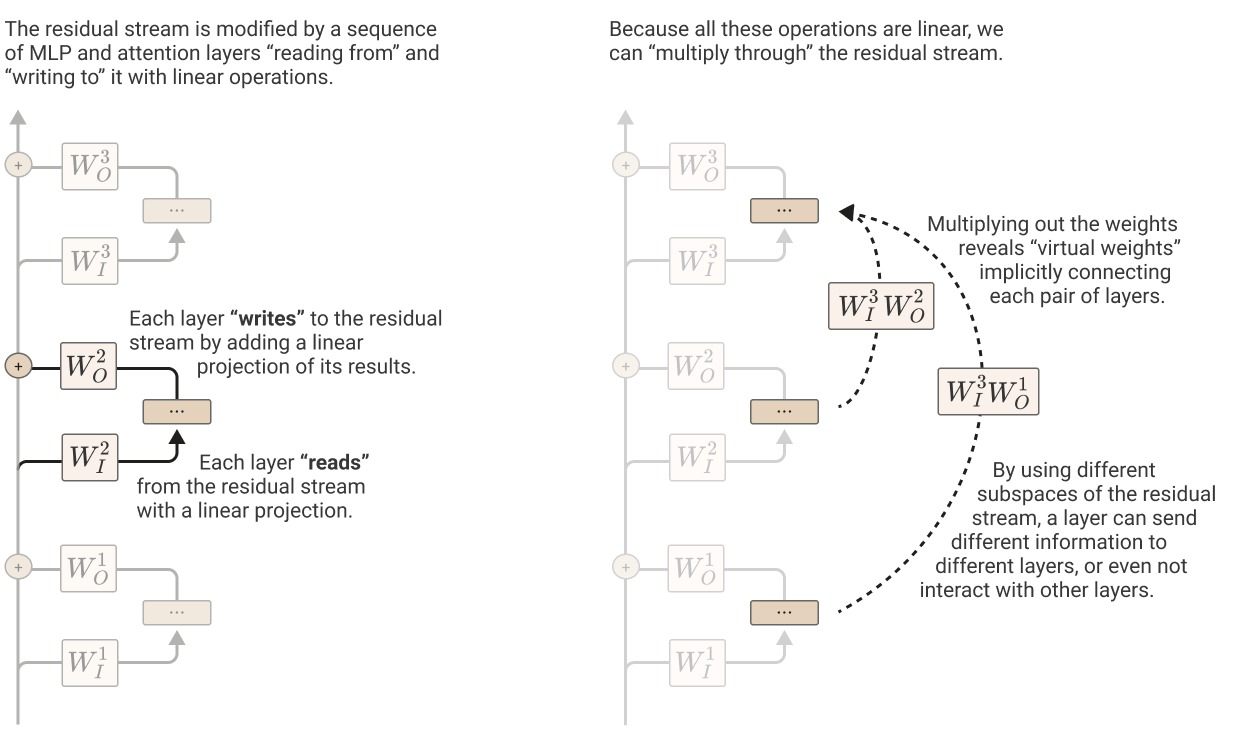
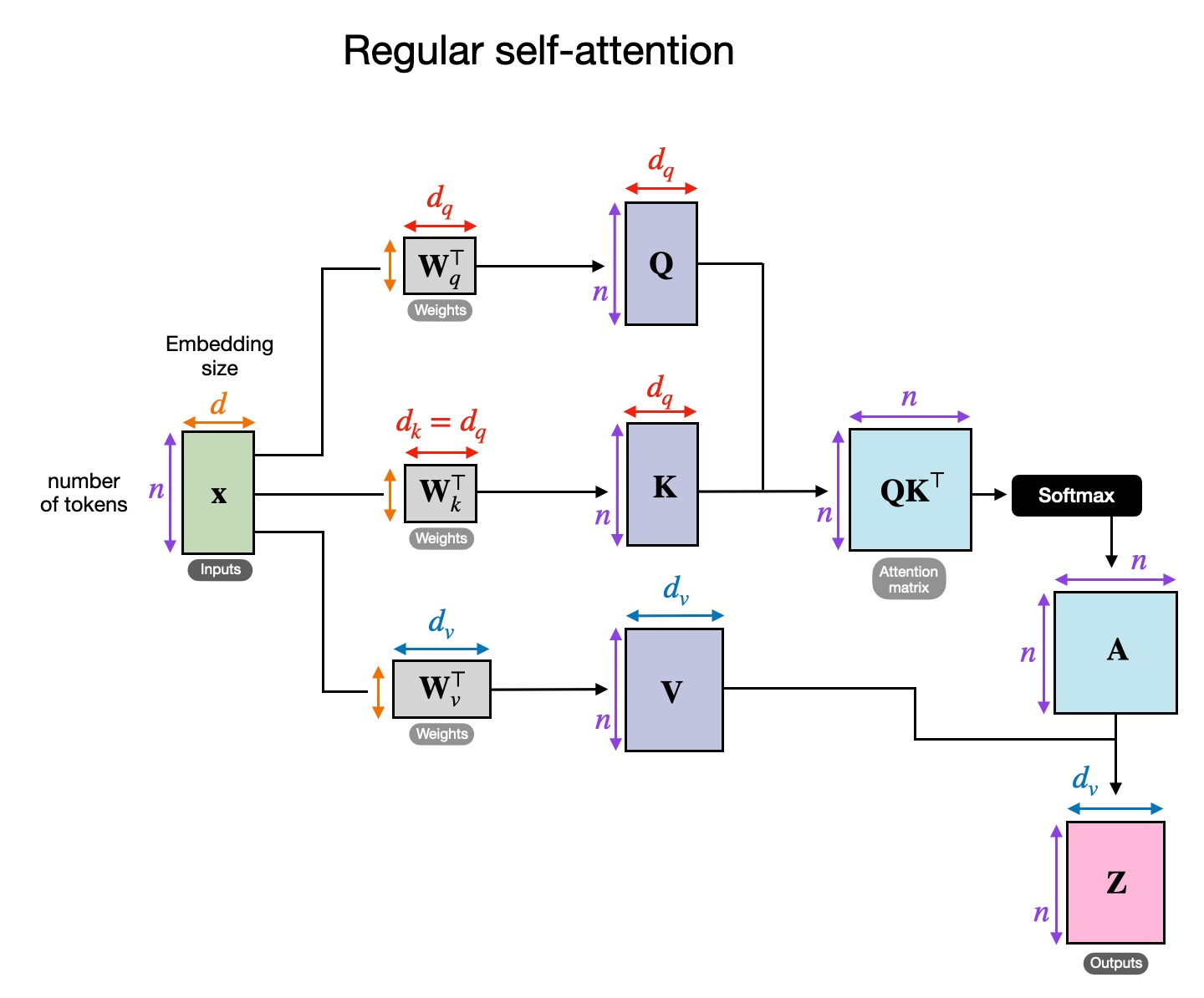
Observations about Attention 4
- Applying attention can be described as
- And the attention pattern is
- and always operate together. They’re never independent. Similarly, and always operate together as well.
- An attention head is really applying two linear operations, and , which operate on different dimensions and act independently.
- governs which token’s information is moved from and to.
- governs which information is read from the source token and how it is written to the destination token.
- Products of attention heads behave much like attention heads themselves. By the distributive property
- These are called virtual attention heads
MLP layers are KV memories 5
Link to original
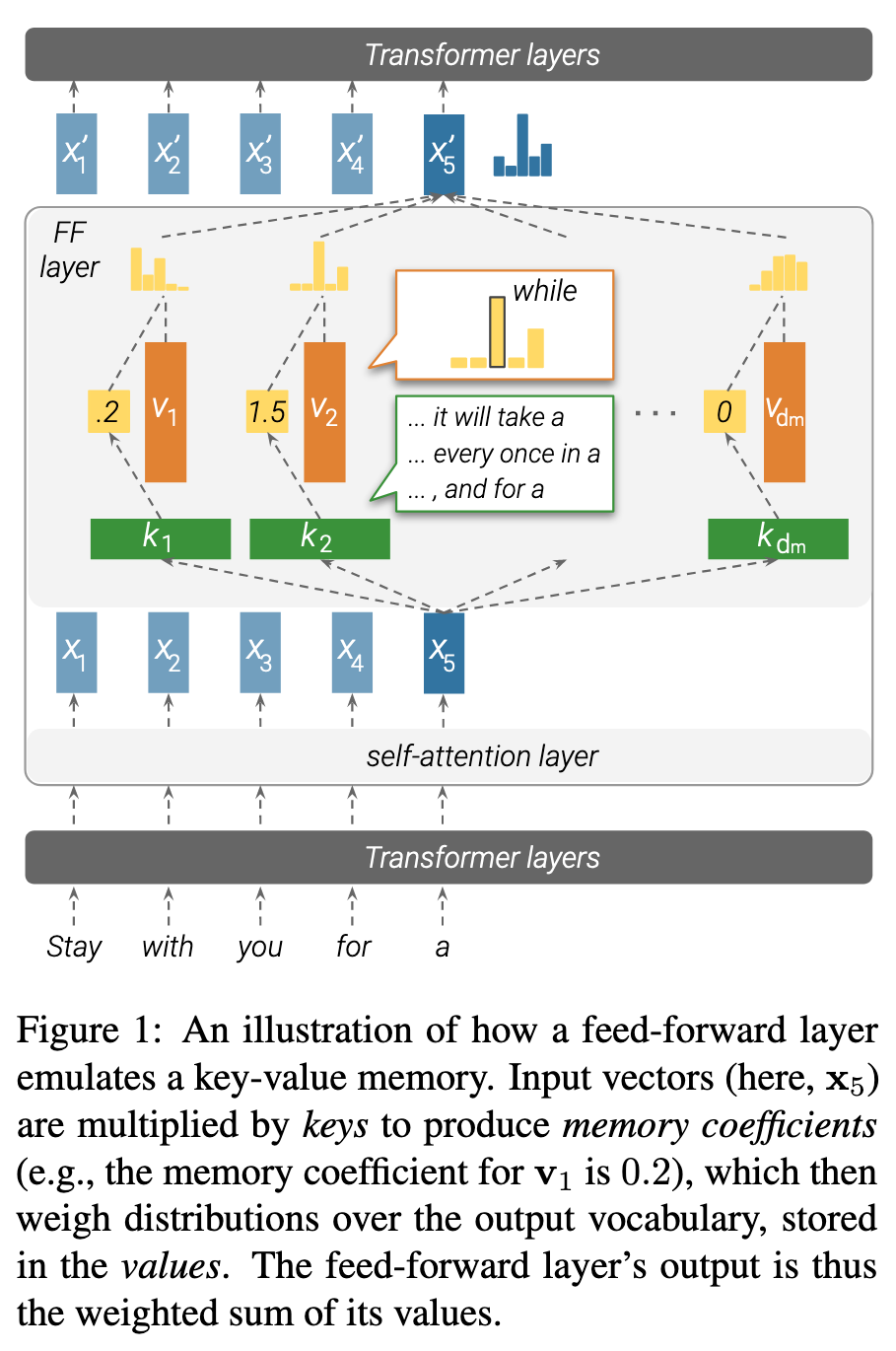
- MLP layers are Unnormalized Key-Value Memories
- MLP layers 6 :
- Neural Memory 7 :
- MLP layers are almost identical to KV neural memories. The only different is
- neural memory uses as the non-linearity
- while MLPs in transformer doesn’t use a normalizing function
- Intra-layer and inter-layer memory composition
“the layer-level prediction is typically not the result of a single dominant memory cell, but a composition of multiple memories.”
Link to original“the model uses the sequential composition apparatus as a means to refine its prediction from layer to layer, often deciding what the prediction will be at one of the lower layers.”
Link to original
Link to original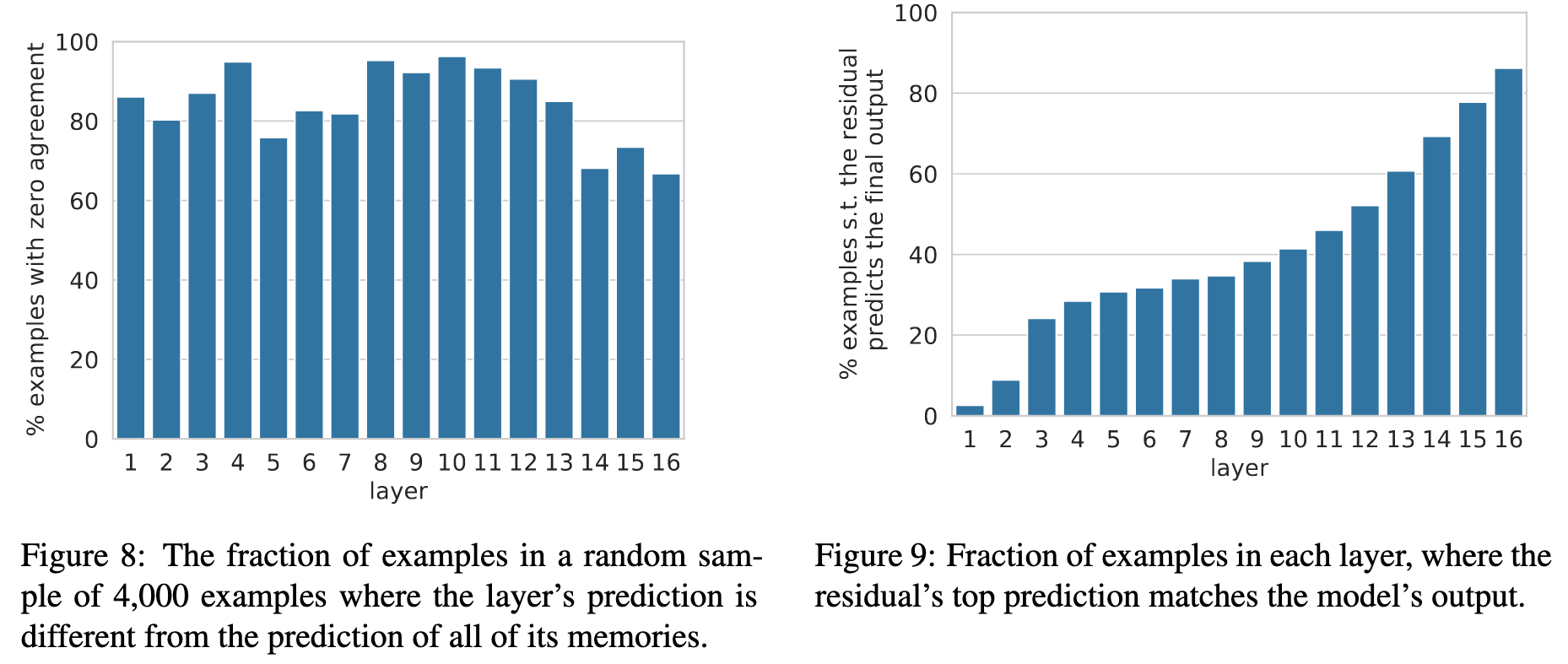
my observations, hypotheses and findings
literature
papers
- Refusal in Language Models Is Mediated by a Single Direction
- The Linear Representation Hypothesis and the Geometry of Large Language Models
- Representation Engineering - A Top-Down Approach to AI Transparency
- Steering Language Models With Activation Engineering
- A Language Model’s Guide Through Latent Space
- Linear Representations of Sentiment in Large Language Models
- Universal and Transferable Adversarial Attacks on Aligned Language Models
- Transformer Feed-Forward Layers Are Key-Value Memories
- Mechanistic Interpretability for AI Safety — A Review
articles
- A Mathematical Framework for Transformer Circuits
- Toy Models of Superposition
- Towards Monosemanticity: Decomposing Language Models With Dictionary Learning
- Transformer Circuits Thread
- Thread: Circuits