Z-function

string

What

Calculate the array z where z[i] = longest common prefix of s and s[i:].

Idea

• use dynamic programming
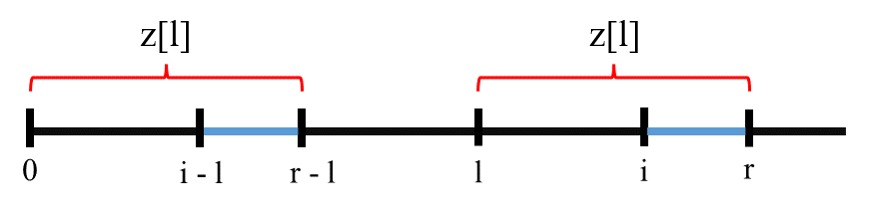
• maintain the interval [l, r] where:
  • s[l : r + 1] == s[:r - l + 1] (s[l...r] is a prefix of s)
  • r is as big as possible
• for each position i , use the interval [l, r] to initialize z[i]:
  • if l <= i <= r then s[l : i] == s[:i - l + 1]
    • because s[l : r + 1] == s[:r - l + 1] (defined above)
  • if i > r then keep as 0
• then try increase z[i] (expand the prefix starts at i) using the naive approach.
• update [l, r] with [i, i + z[i] - 1] if i + z[i] - 1 > r
  • this keeps i > l and increase r as new z[i] is computed.

Implementation

def zfunction(s):
	n = len(s)
	z = [0] * n
 
	# maintain the interval [l, r], where
	# s[l : r + 1] == s[:r - l + 1] and `r` is max
	l, r = 0, 0
 
	# start from 1 because z[0] = n and will make `r` becomes `n - 1`
	# i will always be > l
	for i in range(1, n):
		# initialize z[i] based on info from the interval [l, r]
		# because s[l : r + 1] == s[:r - l + 1]
		# thus s[l : i] == s[:i - l + 1] for l <= i <= r
		if i <= r:
			z[i] = min(z[i - l], r - i + 1)
 
		# trying to extend the match
		while i + z[i] < n and s[z[i]] == s[i + z[i]]:
			z[i] += 1
 
		# update the interval [l, r]
		if r < i + z[i] - 1:
			l, r = i, i + z[i] - 1
 
	return z

Complexity

• Time: $O(n)$
  • r is always increase at each iteration
• Space: $O(n)$

Misc

• This has a similar spirit to LSP - Longest Suffix which is also a prefix.
• Reference: Z-function - VNOI wiki