The effects of neural net layers on activation space

consecutive matrix transformations are series of change of basis in activation space

• initial vector space with basis {python} [1, 0], [0, 1], the yellow region indicates ReLU operation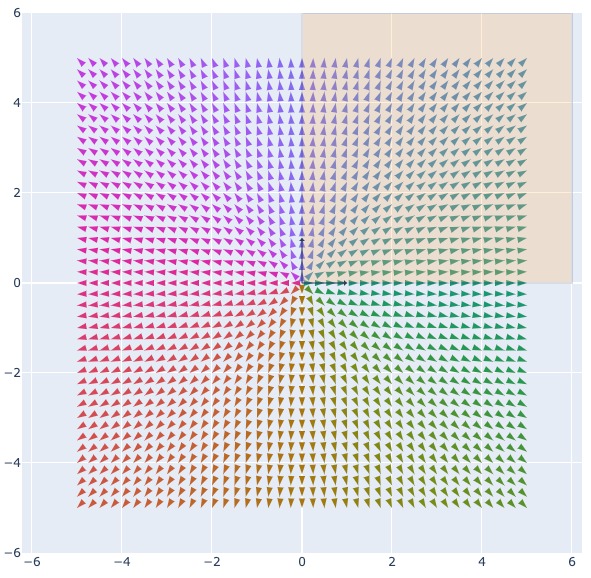
• the vector space after changed to basis {python} [2, -1], [0, 2]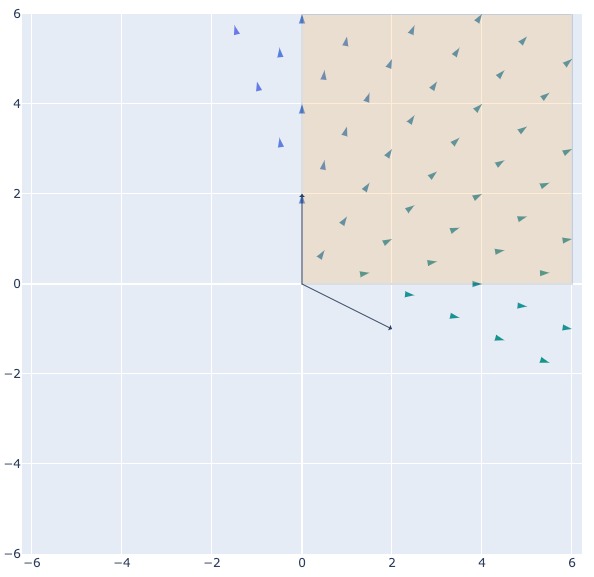

NNs are series of change of basis

• multiplying with a matrix is changing the basis of the vectors (data) space

• skip connection is combining the 1st orthant of the spaces spanned by multiple basis

• applying ReLU is to discard everything but the 1st orthant/hyperoctant (all component is non-negative)

• For a transformer layer:

  • The skip connection is indeed maintain the geometry
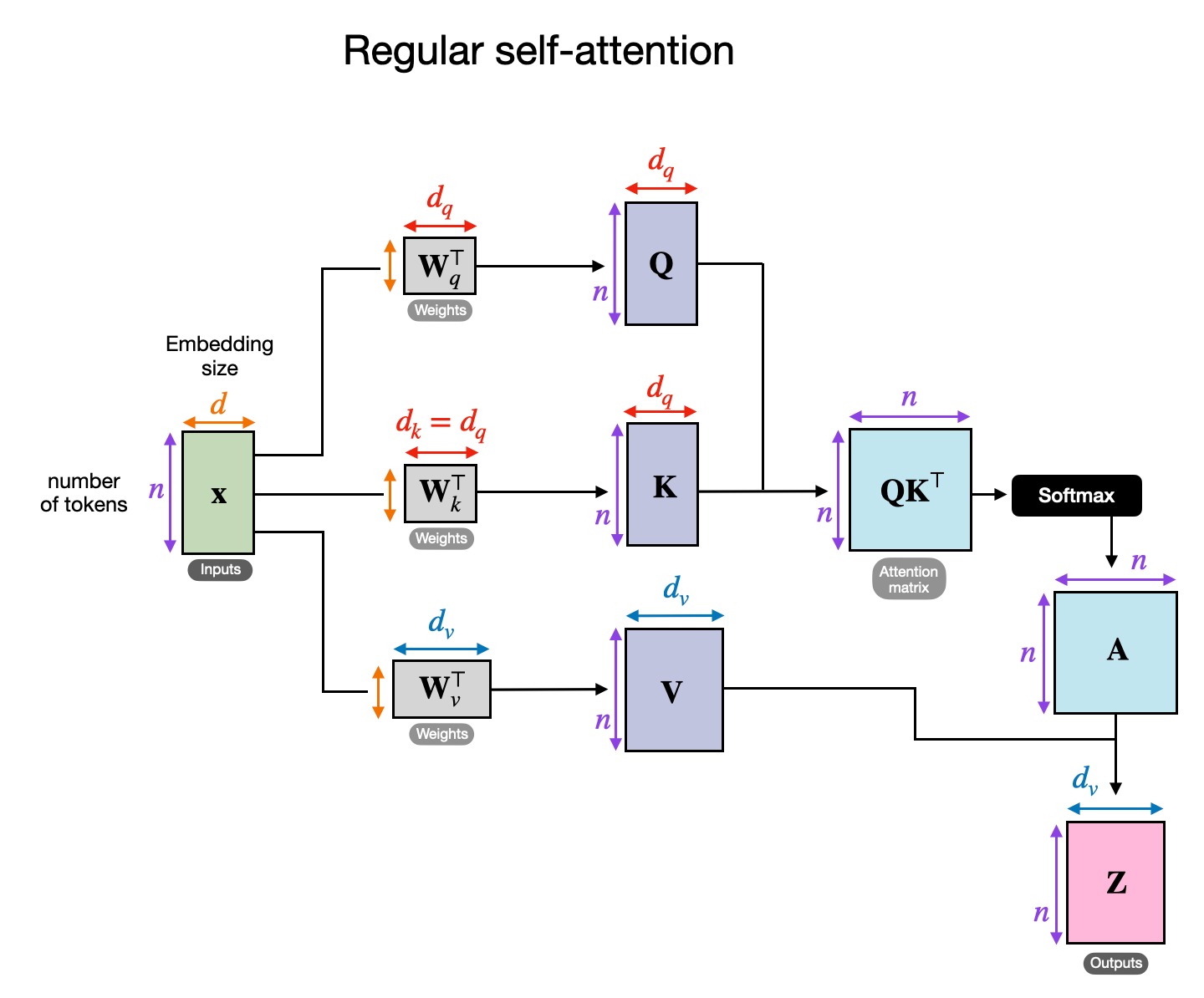
  • In self-attention:
    • When $d==dv$, the values $V$ is $X$ but with different basis vectors (by matrix transformation $W_v$)
      • Each row (token) in $Z$ is a linear combination of each row (token) in $V$ (with the coefficients decided in $A$)
        • Hence $Z$ have the same basis as $V$
      • Hence $X$ and $Z$ are both in Euclidean space but with different basis
      • Hence even with a softmax operation, transformer blocks are still a change of basis operation
  • So the attention layer learn a set of basis based on the tokens within the attention window
  • By applying the skip connection, the output activations can be seen as combinations by 2 set of basis (with and without attention)
    • as layer went deeper, the activations become the combinations of more and more basis vectors, each of which might represent different knowledge/behaviourhypothesis
    • 

transformer layers expand and “untangle” the activation space

transformer layers expand and “untangle” the activation space

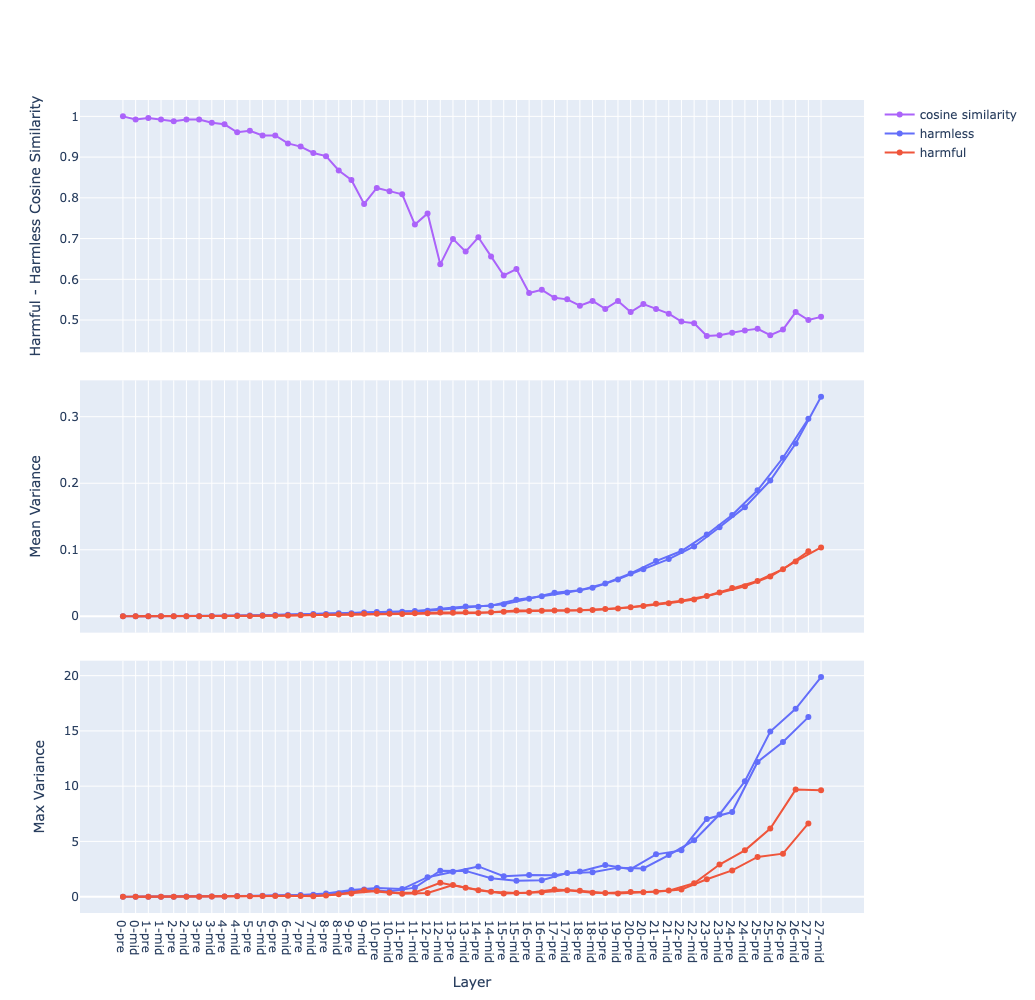
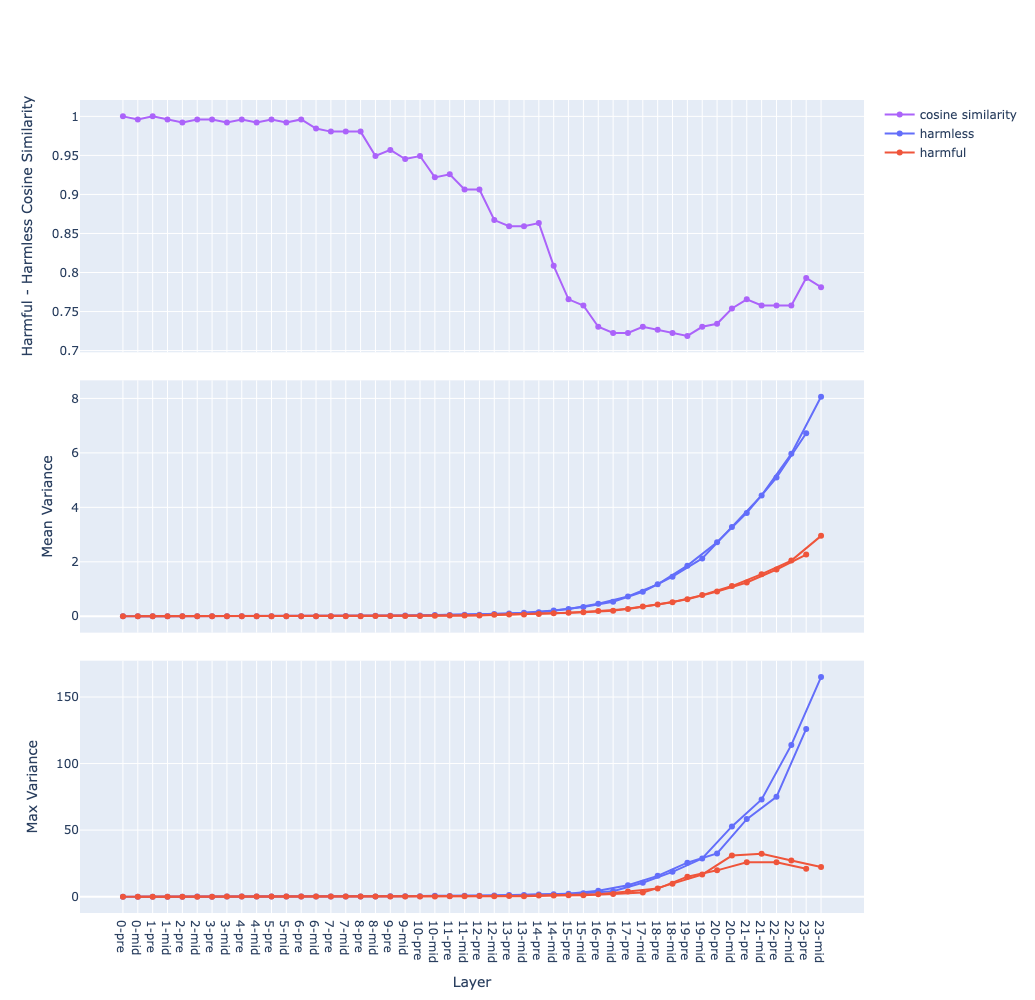
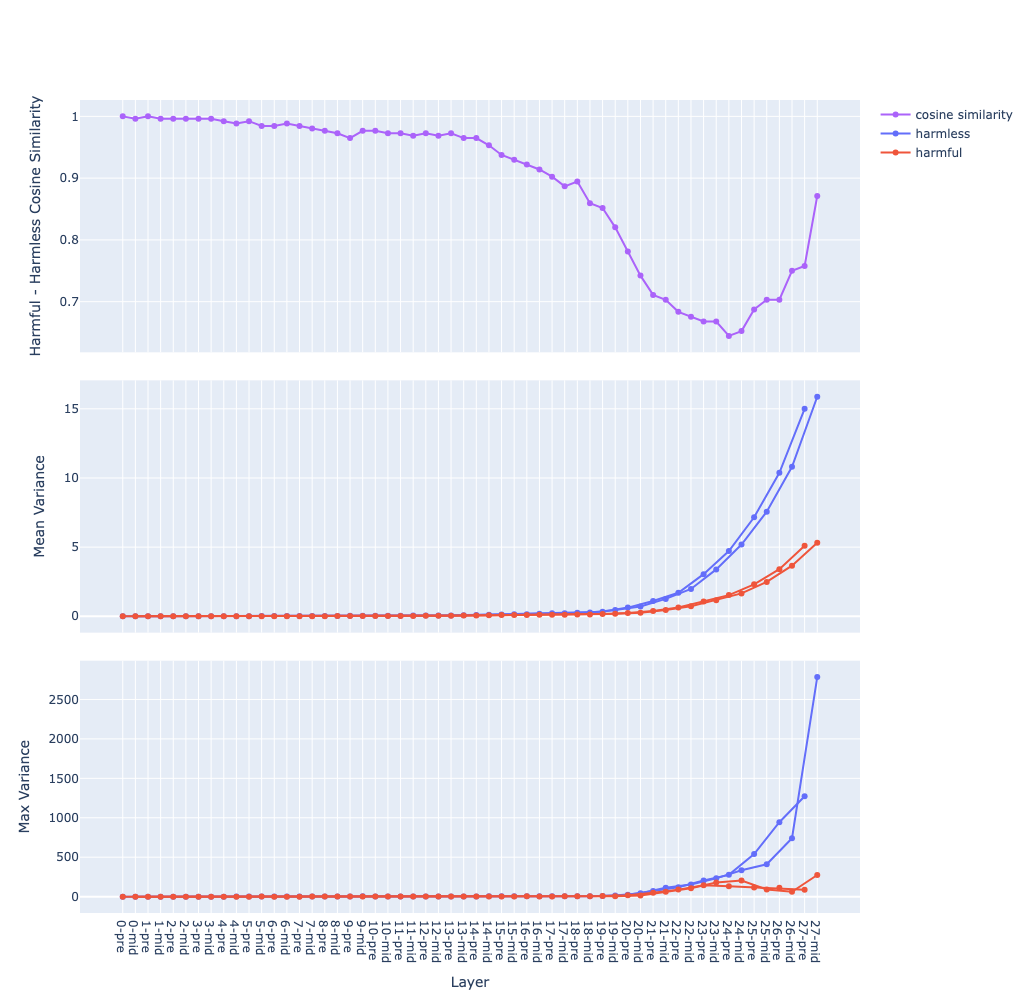
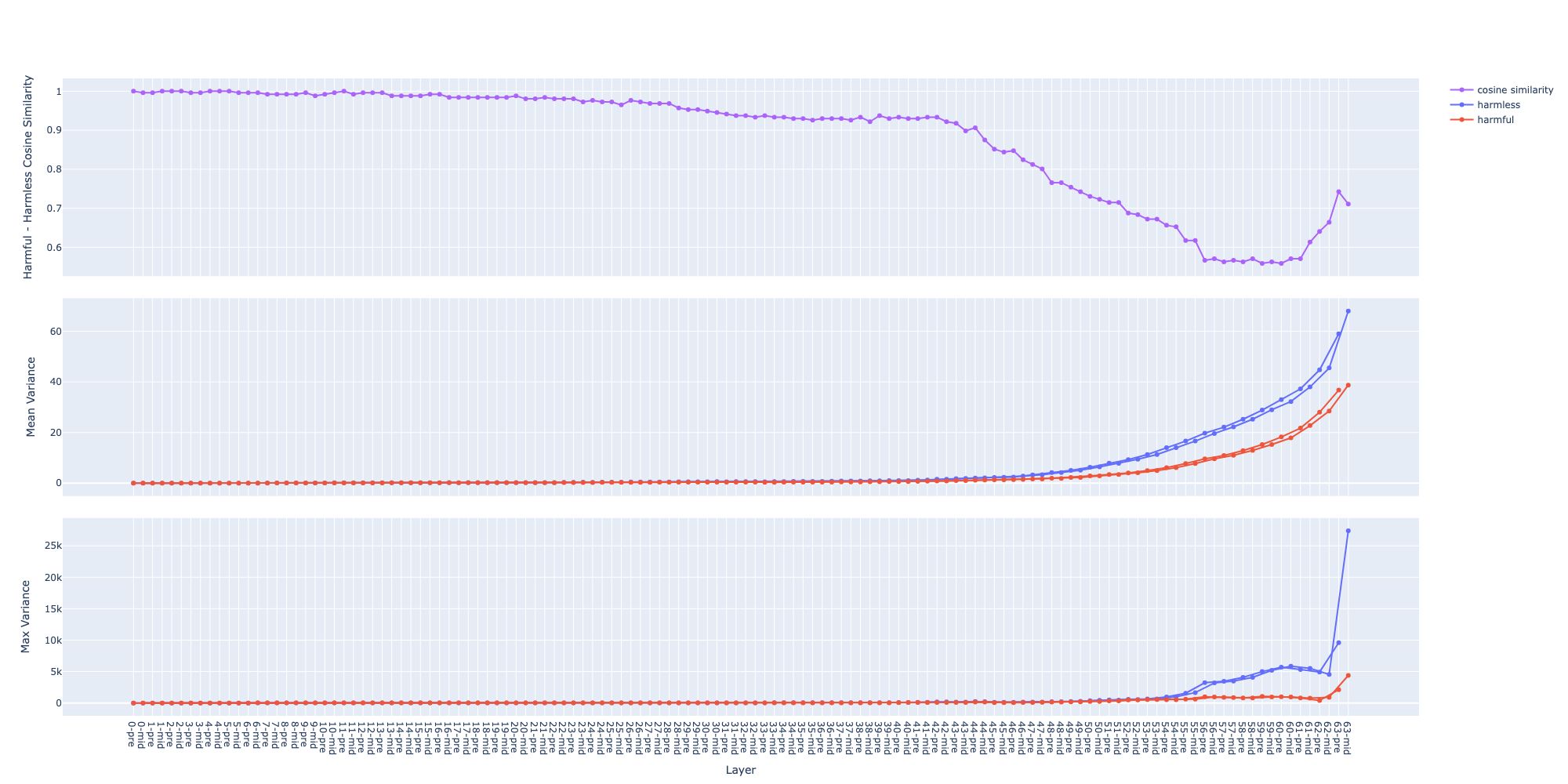
Steps to compute these graphs:

• data sets: 2 contrastive data sets, in this case are harmful and harmless

• feed each data sets through the model and capture activations

  • at each residual stream²
  • at each layer
  • at the last token → we get 2 matrices P (positive) and N (negative) of size samples x layers x features

• the top graph:

  • compute the mean vector for each data sets: X_mean = X.mean(dim=0) → we get 2 matrices P_mean and N_mean of size layers x features
  • compute the cosine similarity between the 2 vectors at each layer (e.g. P_mean[l] and N_mean[l]), we get a vector of size 1 x layers similarity_score = cosine_similarity(P_mean, N_mean, dim=-1)

• the middle graph:

  • compute the variance vector for each data sets: X_var = X.var(dim=0) → we get 2 matrices P_var and N_var of size layers x features
  • then compute the mean along the feature dimension, we get 2 vectors of size 1 x layers: P_var_mean = P_var.mean(dim=-1) N_var_mean = N_var.mean(dim=-1)
  • 2 curves of the same colour are for 2 residual streams, in this case are pre and mid

• the bottom graph: same as the middle one but for max instead of mean

Observations, questions and hypotheses

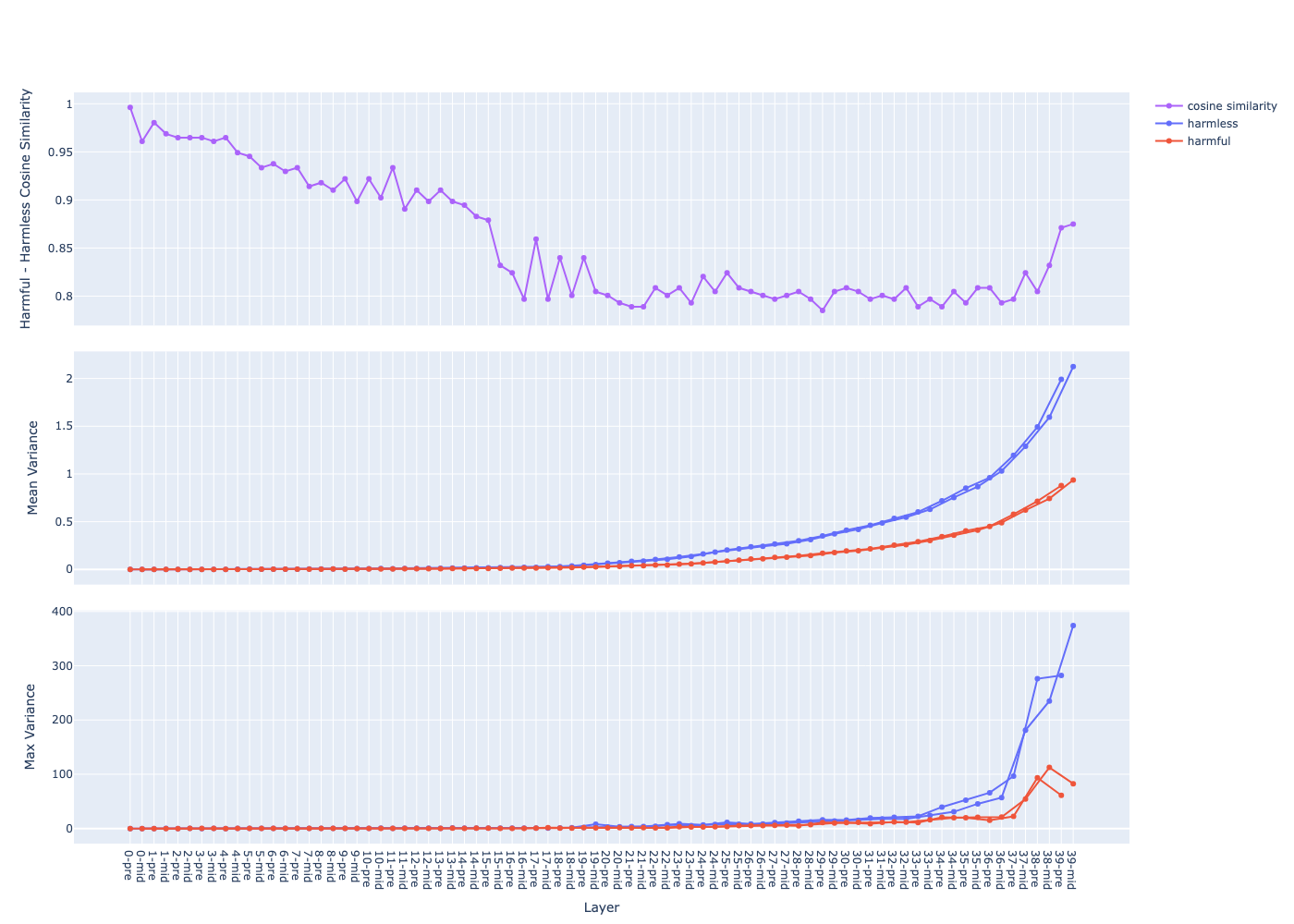
• The mean of variance (the middle graph) grows in a near-exponential trajectory from the first to last layerobservation why ?question

  • The growth of pre(before attention) and mid(after attention) streams are separatedobservation why ?question
  • Hypothesis:hypothesis
    • the model start with an initial state (the activation of the 1st layer) near the origin (due to input vector and the weights are usually between 0 and 1)
    • each layer move the current state (the activation) through the activation space in some directions
    • the directions are similar between layers, hence the state goes further and further along those directions
    • suppose that the amount moved by each layer is within a similar range (due to layer norm), then distance travelled (the norm of the activation vector) grows linearly
    • hence the variance (distance squared) grows exponentially
  • we can analyze this by checking for shared directions between the weights across layersexperiment

• Transformer layers expand and “untangle” the activation space the deeper we gohypothesis

  • different samples would be aligned in different directions, hence they move further away

Visualization on several models of different sizes and families

• Llama 3.2 3B

• Qwen 1 8B

• Qwen 2.5 7B

• Qwen 2.5 32B

• Mistral-Nemo-Instruct-2407 (12B)

Link to original