The Reparameterization trick

theory

what

• A method for computing/estimating gradients of random variables

  • Because we cannot take the derivative of a random variable
  • Reparameterization “restructures” the problem so that it’s differentiable (source ¹, ²)

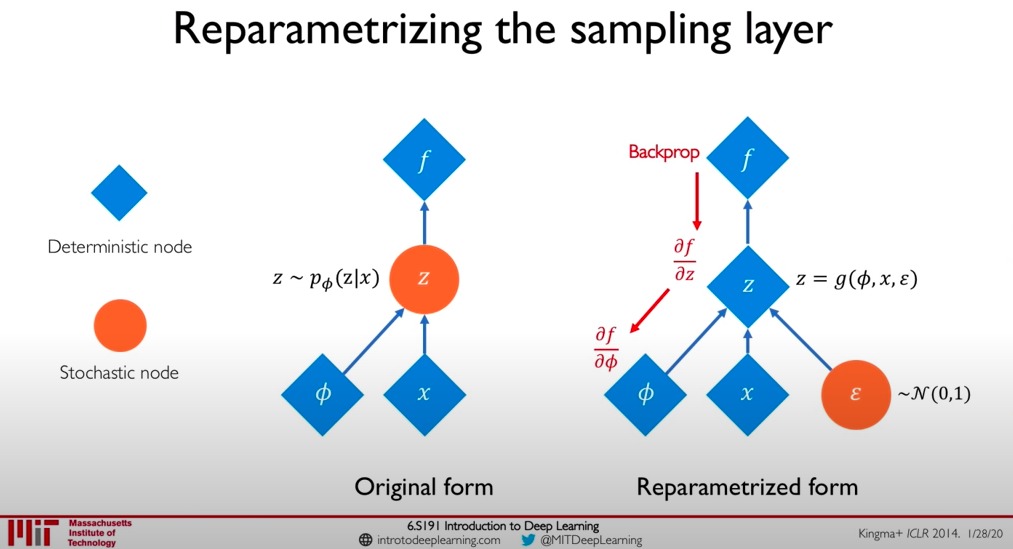
• Most widely refers to the case of sampling from a normal distribution from a standard normal distribution using the following formula:

  $$x=\mu +\sigma \cdot z$$

  where $z$ is drawn from $\mathcal{N}(0,1)$.

• Reparameterization is a method of generating non-uniform random numbers by transforming some base distribution, $p(ϵ)$, to a desired distribution, $p(z;\theta )$. The transformation from the base to the desired distribution can be written as $g(ϵ;\theta )$, as follows ³:

  $$p(ϵ)\to g(ϵ;\theta )\to p(z;\theta )$$

why

• We use the reparameterization trick to express a gradient of an expectation $(1)$ as an expectation of a gradient $(2)$. Provided $g_{\theta }$​ is differentiable - something Kingma⁴ emphasizes - then we can then use Monte Carlo methods to estimate ${\nabla }_{\theta }{\mathbb{E}}_{p_{\theta }(z)}[f(z^{(i)})]$ $(3)$. ⁵

  $$\begin{array}{rlr}ϵ& \sim p(ϵ)& \\ & & \\ z& =g_{\theta }(ϵ,x)& \\ & & \\ {\mathbb{E}}_{p_{\theta }(z)}[f(z^{(i)})]& ={\mathbb{E}}_{p(ϵ)}[f(g_{\theta }(ϵ,x^{(i)}))]& \\ & & \\ {\nabla }_{\theta }{\mathbb{E}}_{p_{\theta }(z)}[f(z^{(i)})]& ={\nabla }_{\theta }{\mathbb{E}}_{p(ϵ)}[f(g_{\theta }(ϵ,x^{(i)}))]& (1)\\ & ={\mathbb{E}}_{p(ϵ)}[{\nabla }_{\theta }f(g_{\theta }(ϵ,x^{(i)}))]& (2)\\ & \approx \frac{1}{L}\sum _i^L{\nabla }_{\theta }f(g_{\theta }({ϵ}^{(l)},x^{(i)}))]& (3)\end{array}$$

• The issue is not that we cannot backprop through a “random node” in any technical sense. Rather, backproping would not compute an estimate of the derivative (because ${\nabla }_{\theta }{\mathbb{E}}_{p_{\theta }(z)}[f(z^{(i)})]$ is the gradient w.r.t. $\theta$ over the expectation w.r.t. $\theta$). Without the reparameterization trick, we have no guarantee that sampling large numbers of z will help converge to the right estimate of ${\nabla }_{\theta }$. ⁵

• The “trick” part of the reparameterization trick is that you make the randomness an input to your model instead of something that happens “inside” it, which means you never need to differentiate with respect to sampling (which you can’t do). ⁶

notes

• Some commonly used reparameterizations (source ¹, ⁷)
• multiple groups realized this fact at the same time around 2013: Rezende et al., Titsias & Lazaro-Gredilla., Kingma & Welling⁴. (All three papers were published in 2014. However, it’s usually the VAE paper that gets all the credit, ⁷

references

Footnotes

1. The Reparameterization Trick – Emma Benjaminson – Data Scientist ↩ ↩²

2. MIT 6.S191 (2020): Deep Generative Modeling - YouTube ↩

3. Machine Learning Trick of the Day (4): Reparameterisation Tricks – The Spectator ↩

4. Auto-Encoding Variational Bayes ↩ ↩²

5. The Reparameterization Trick ↩ ↩²

6. ELI5: The Reparameterization Trick : r/MachineLearning ↩

7. [D] Clarification on the “Reparameterization Trick” in VAEs and why it is a trick : r/MachineLearning ↩ ↩²