generate primes

mathprime

algorithms

sieve of Eratosthenes

classic

def sieve(limit):
    import math
    check = [True] * max(3, limit + 1)
    check[0] = False
    check[1] = False
    check[2] = True
 
    for i in range(4, len(check), 2):
        check[i] = False
    
    sqrt_limit = int(math.sqrt(limit))
    for i in range(3, sqrt_limit + 1, 2):
        if not check[i]:
            continue
        for j in range(i * i, len(check), i):
            check[j] = False
 
    return [i for i in range(limit + 1) if check[i]]

segmented

def segmented_sieve(limit):
    import math
    sieve_size = 10000
    
    sqrt_limit = int(math.sqrt(limit))
    primes = [2]
    is_prime = [True] * (sqrt_limit + 1)
    for x in range(3, sqrt_limit + 1, 2):
        if not is_prime[x]:
            continue
        primes.append(x)
        for m in range(x * x, sqrt_limit + 1, x):
            is_prime[m] = False
    del is_prime
 
    for start in range(0, limit + 1, sieve_size):
        cur_size = min(sieve_size, limit + 1 - start)
        block = [True] * cur_size
        for p in primes:
            i = p * (start // p + bool(start % p)) - start
            while i < cur_size:
                block[i] = False
                i += p
 
        if start == 0:
            block[0] = False
            block[1] = False
 
        for i in range(0, cur_size):
            if block[i]:
                primes.append(start + i)
 
    return primes

references

• Sieve of Eratosthenes - Algorithms for Competitive Programming

trial division

def trial_div(limit):
    import math
 
    all_primes = [2]
 
    for i in range(3, limit + 1, 2):
        is_prime = True
        root = int(math.sqrt(i))
        for p in all_primes:
            if p > root:
                break
            if i % p == 0:
                is_prime = False
                break
        if is_prime:
            all_primes.append(i)
 
    return all_primes

Dijkstra

def dijkstra(limit):
    multiples = [4]
    all_primes = [2]
    lim_prime_idx = 0  # index of the smallest prime doesn't need to check
 
    for x in range(3, limit + 1, 2):  # skip 2
        if x >= multiples[lim_prime_idx]:
            lim_prime_idx += 1
            # next prime already found due to p_{n + 1} < p_{n}^2
            multiples.append(all_primes[lim_prime_idx]**2)
 
        is_prime = True
        for i in range(1, lim_prime_idx):  # skip 2
            if multiples[i] < x:
                multiples[i] += 2 * all_primes[i] # only odd multiples
            if x == multiples[i]:
                is_prime = False
                break
 
        if is_prime:
            all_primes.append(x)
 
    return all_primes

intuition

• fox x in range (primes[i - 1]**2, primes[i]**2) with primes[i - 1] and primes[i] are consecutive primes
  • only need to check for prime factors < primes[i]
  • open conjecture: there is a prime number in between the squares of 2 consecutive primes
    • related to Legendre’s conjecture
• to check for composites, maintain a list of multiples of all primes up to primes[i]
  • multiples[i] is the smallest multiple of the primes[i] that >= x
  • only need to extend multiples when the range (primes[i - 1]**2, primes[i]**2) changes
  • multiples[i] is initialized with primes[i]**2 because smaller multiples of primes[i] is divisible by some prime < primes[i]

visualization

![[assets/generate primes/attachment.jpg]]
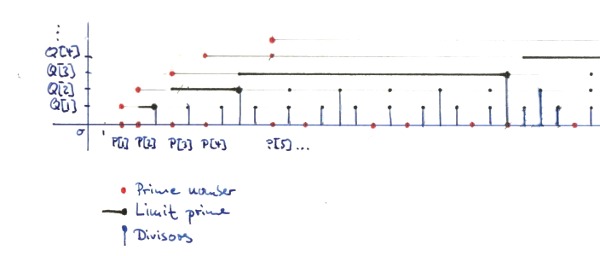(`Q` is the list of multiples, index starts from 1)

references

• Dijkstra’s Hidden Prime Finding Algorithm - YouTube
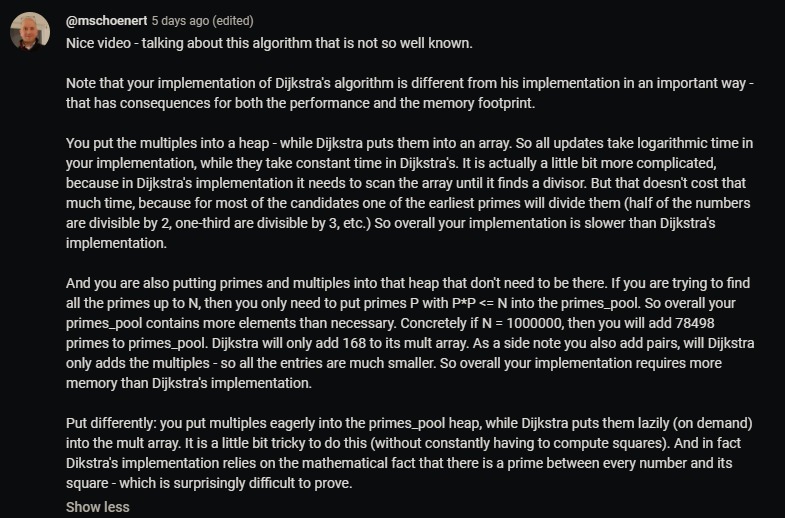
  • also check the comments
• Dijkstra’s Prime Number Algorithm
• cs.utexas.edu/users/EWD/ewd02xx/EWD249.PDF
• relies on the mathematical fact that there is a prime between every number and its square - which is surprisingly difficult to prove (see Bertrand’s theorem).

performance comparison

import time
import tracemalloc
 
limit = 10**6
 
def profile(func, limit):
    t = time.perf_counter()
    primes = func(limit)
    print("num primes:", len(primes))
    print("time:", time.perf_counter() - t)
    
    tracemalloc.clear_traces()
    tracemalloc.start()
    func(limit)
    cur, peak = tracemalloc.get_traced_memory()
    tracemalloc.stop()
    print("memory:", peak - cur)
    print()
 
print('sieve', '-' * 10)
profile(sieve, limit)
 
print('segmented sieve', '-' * 10)
profile(segmented_sieve, limit)
 
print('trial div', '-' * 10)
profile(trial_div, limit)
 
print('dijkstra' , '-' * 10)
profile(dijkstra, limit)

sieve ----------
num primes: 78498
time: 0.3589751999825239
memory: 11143176
 
segmented sieve ----------
num primes: 78498
time: 1.2164868999971077
memory: 3280104
 
trial div ----------
num primes: 78498
time: 1.4015573000069708
memory: 3143152
 
dijkstra ----------
num primes: 78498
time: 0.9058849000139162
memory: 3149888